MODEL PITA ENERGI
BAB
II
PEMBAHASAN
2.1
Teori Pita Energi
Semikonduktor
adalah sebuah bahan dengan konduktivitas listrik yang berada di antara isolator
dan konduktor. Semikonduktor disebut juga sebagai bahan setengah penghantar
listrik. Bahan semikonduktor yang sering digunakan adalah silicon, germanium,
dan gallium arsenide. Silikon dan Germanium adalah bahan semikonduktor yang
paling banyak digunakan daripada Germanium karena sifatnya lebih stabil pada
suhu tinggi. Silikon adalah material dengan struktur pita energy tidak langsung
(indirect bandgap), di mana nilai minimum dari pita konduksi dan nilai maksimum
dari pita valensi tidak bertemu pada satu harga momentum yang sama. Ini berarti
terjadi eksitasi dan rekombinasi dari pembawa muatan diperlukan perubahan yang
besar pada nilai momentumnya atau dapat dikatakan dibutuhkan bantuan sebuah
partikel dengan momentum yang cukup untuk mengkonservasi momentum pada semua
proses transisi. Dengan kata lain, silicon sulit memancarkan cahaya. Sifat ini
menyebabkan silicon tidak layak digunakan sebagai piranti
fotoni/optoeloktronik.
Kristal
adalah susunan atom-atom molekul dalam ruang yang dibangun dengan mengadakan
pengulanganstruktur satuan dasar dalam tiga dimensi. Karena jarak antar atom
dalam zat padat berdekatan satu sama lain maka antara atom yang satu dengan
yang lain terjadi interaksi. Akibatnya keadaan tingkat energy akan berbeda
dengan keadaan tingkat energy atom terisolasi. Untuk atom-atom yang membentuk
kristal ternyata tingkat energy dari electron-elektron pada kulit dalam tidak
berubah, tetapi tingkat tenaga electron pada kulit terluar berubah karena
electron-elektron tersebut menjadi milik bersama lebih dari satu atom dalam
kristal. Tingkat energy electron pada kulit terluar tersebut berubah menjadi
pita, seperti ditunjukkan pada gambar 1.
Gambar 1. Skema Pita Energi
Jika seperti dalam skema gambar 1, sebuah pita
benar-benar terisi penuh dengan electron dan pita yang tepat diatasnya kosong,
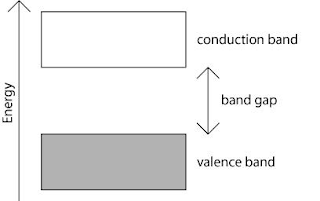
maka material tersebut memiliki celah pita energy. Celah pita energy ini adalah
perbedaan energy antara pita valensi dan pita konduksi. Elektron dalam logam
juga disusun dalam pita, tetapi dalam logam distribusi electron berbeda,
electron tidak terisolasi. Dalam logam sederhana dengan satu electron valensi
per atom, seperti natrium, pita valensi tidak terisi penuh, sehingga terdapat
tempat tertinggi bagi electron untuk menduduki tingkat keadaan tersebut. Bahan
tersebut merupakan konduktor listrik yang baik, karena ada keadaan energy
kosong yang tersedia, sehingga electron dapat dengan mudah memperoleh energy
dari medan listrik dan melompat ke keadaan energy yang kosong.
Beberapa hal yang perlu
diperhatikan pada model pita energy yaitu:
1. Ada energy potensial periodic V
(͞r͞) yang tidak sama dengan nol di dalam kristal dengan keberkalaan kisi
kristal
2. Fungsi gelombang Ψ (r͞ ) dibuat berdasarkan kisi yang sempurna, tidak
mengenal cacat geometric, tidak mengenal ketakmurnian, dan dimana dianggap kisi
tidak melakukan getaran termal.
3. Teori pita energy dikembangkan sebagai teori electron tunggal, dimana
di telaah perilaku satu electron di bawah pengaruh suatu potensial periodic V (͞r͞) yang merepresentasikan semua
interaksi baik dengan ion-ion kristal maupun semua electron yang lain.
4. Teori electron tunggal berarti bahwa dapat dipergunakan persamaan
Schroedinger untuk satu electron:
Gambar 2. Skema Pita Energi
Isolator, Semikonduktor, dan Konduktor
2.2 Teorema Bloch
Teorema Bloch dipergunakan untuk menyelesaikan potensial berulang
secara periodic, yaitu dengan memodifikasi fungsi gelombang electron bebas
dengan fungsi potensial periodic. Bloch menyelesaikan persamaan gelombang
Schroedinger electron dengan memasukkan syarat bagi fungsi potensial yang
memiliki sifat periodic seperti yang terdapat dalam kristal. Dalam penelaahnya
itu potensial periodic V (r͞ ) merupakan superposisi dari dua bagian,
yaitu sebagai berikut:
1.
Potensial berkala dari kisi-kisi gugus-gugus atom atau ion.
2.
Potensial yang berasal dari semua electron terluar atom – atom, dianggap bahwa
rapat muatan electron-elektron termaksud mempunyai harga rata-rata yang identic
untuk setiap sel satuan dalam kristal.
Fungsi gelombang Schroedinger ketika ada
potensial periodik untuk keberkalaan kisi adalah:

Dengan  merupakan fungsi yang memiliki keberkalaan kisi
kristal.
merupakan fungsi yang memiliki keberkalaan kisi
kristal.
Gambar Sketsa Potensial Periodik untuk
Kisi Linier Monoatomik
Kita perhatikan persamaan Schroedinger untuk satu electron dalam
potensial seperti di atas, maka:

Kesimpulan dari
persamaan di atas adalah:
1. Untuk setiap X akan di dapat Ψ yang berulang setelah N buah
sel satuan. Panjang kristal I=Na,
sehingga didapat; 
2. Fungsi gelombang electron bebas dalam satu dimensi adalah  untuk potensial nol. Untuk
potensial yang tidak nol fungsinya
untuk potensial nol. Untuk
potensial yang tidak nol fungsinya  .
.
Dari fungsi  di dapat
di dapat  yan merupakan fungsi periodic dengan keberkalaan a.
yan merupakan fungsi periodic dengan keberkalaan a.
Teorema Bloch untuk satu
dimensi menyatakan ciri-ciri fungsi gelombang untuk suatu potensial berkala
dalam ruang satu dimensi. Hal ini dapat diperluas untuk ruang dimensi tiga
sehingga berlaku umum. Teorema Bloch hanya menyatakan sifat Ψ (x) dan tidak
menyelesaikan persamaan Schroedinger untuk electron dalam suatu zat padat.
2.3 Model
Kronig-Penney
Model Kronig-Penney
menelaah perilaku electron dalam kristal linier sederhana meskipun tidak
menyelesaikan masalahnya secara konkret, tetapi memberikan ciri-ciri yang pokok
tentang perilaku electron dalam potensial periodic. Model Kronig-Penney
menelaah gerak electron dalam suatu potensial berkala seperti gambar di bawah
ini:
Gambar Model Potensial Kronig-Penney
dari Kristal
Agar dapat menyelesaikan
persoalan ini, harus dipilih fungsi gelombang yang dapat mewakili sifat-sifat
electron. Fungsi gelombang yang berhubungan dengan potensial periodic ini akan
memenuhi persyaratan yang ada pada teorema Bloch. Jika V (x) mempunyai periode ( ) dengan pperincian potensial sebagai berikut:
) dengan pperincian potensial sebagai berikut:
a. V= 0 di daerah 0 < x< 
b. V= V0 di daerah 
Persamaan Schroedinger
untuk electron tunggal adalah sebagai berikut:

Kita membatasi diri pada
solusi dengan energy E< V0. Untuk dapat menelaah berikutnya, kita
bataskan dua besaran riel,  dan
dan  :
:
Dengan mensubstitusikan
solusi umum dari teorema Bloch ke persamaan Schrodinger akan didapatkan;

Dengan solusi
Penyelesaian determinan
tersebut mempersyaratkan bahwa:
Di bawah ini adalah sketsa ramalan harga energy electron
pada potensial periodic kristal monoatomic linier dan kaitan model
Kronig-Penney dengan harga energy untuk electron bebas dan electron dalam kotak
potensial berdinding tak hingga.
Struktur level energi untuk derajat ikatan yang berbeda.
Daerah yang tidak mempunyai solusi
adalah daerah terlarang sehingga di daerah ini persamaan Schroedinger tidak
memberikan solusi bagi Ψ (x). Energi yang sesuai dengan daerah  yang terlarang itu, merupakan harga energi
yang terlarang
yang terlarang itu, merupakan harga energi
yang terlarang
2.4 Model Elektron Hampir Bebas (Model Kisi Kosong)
Model elektron bebas mengasumsikan potensial kristal sangat
lemah sehingga elektron berperilaku hampir bebas. Istilah kisi kosong di sini
artinya meskipun potensial kristal dianggap sama dengan nol, tetapi fungsi
gelombang yang merupakan solusi persamaan Schroedinger menaati sifat
kesetangkupan kisi kristal. Persamaan untuk elektron ini adalah:

Spektrum  kontinu, seperti pada gambar :
kontinu, seperti pada gambar :
Gambar (a) menunjukkan extended zone
Gambar (b) menunjukkan reduced zone
Gambar (c) menunjukkan Brillouin zone
I.
Di sini tidak ada pembatasan energi sehingga spektrum energinya kontinu. Model
kisi kosong ini membantu dalam memahami model elektron hampir bebas.
Model elektron bebas
mengasumsikan potensial kristal lemah tetapi tidak sama dengan nol. Berdasarkan
teorema Bloch untuk kristal satu dimensi, diskontinuitas energi elektron pada
batas-batas brillouin zone yaitu untuk  . Daerah ini terdapat pada gambar:
. Daerah ini terdapat pada gambar:
Gambar (a) daerah reduced zone
Gambar (b) daerah extended zone
Loncatan antara dua daerah
energi disebut energi gap. Untuk mengevaluasi besarnya energi gap
ini digunakan teori PETURBASI. Yang persamaannya adalah;

2.5 Logam, Isolator, dan
Semikonduktor
Suatu presentasi secara
skematik energy electron E terhadap k, untuk model Kronig-Penney, tertera pada
grafik di bawah. Grafik E = E(k)
memperlihatkan daerah energy yang diperkenankan dan terlarang bagi electron. Tetapi
energy ini masih bergantung pada jumlah electron dalam kristal dan statistika
energy electron.
Gambar Grafik Hubungan Antara Energi terhadap k untuk Model
Kronig-Penney
Perlu diingat bahwa
model Kronig-Penney yang digunakan adalah model satu dimensi dengan keberkalaan
(a + b). Grafik E=E(k) tersebut memperlihatkan daerah-daerah harga energy
electron yang diperkenankan dan pula daerah-daerah terlarang bagi harga energy
electron.
Daerah-daerah kerja
energy yang diperkenankan sesungguhnya merupakan electron states yang tersedia
bagi elekton dalam kristal. Apakah electron states tersebut memang dihuni oleh
electron masih bergantung dari jumlah electron dalam kristal dan statistika
elektronnya. Ada dua hal dimana medan listrik luar tidak menghasilkan arus
netto electron dalam kristal, yaitu apabila:
1. Pita energy yang diperkenankan sama sekali tidak dihuni oleh electron.
2. Pita energy yang diperkenankan terisi penuh dengan electron, artinya
semua electron states yang ada terisi dengan electron.
Sekarang kita telaah
perilaku satu electron dalam pita yang kosong. Artinya, hanya ada satu electron
dalam pita tersebut. Dalam gambar di bawah ini electron dipresentasikan dengan
A.
Gambar Sketsa Perilaku Elektron dalam Pita Kosong
Akibat medan listrik elektron di A
akan bergerak ke arah –X dan sampai pada kedudukan A’. Pada saat itu
terjadi pantulan Bragg, dan elektron muncul kembali di A’. Kemudian
elektron menempuh siklus yang sama. Proses berulang ini disebut sebagai osilasi
Zener.
Rapat arus yang disumbangkan oleh pita
energi yang tidak seluruhnya penuh, diberikan oleh persamaan;
Model pita energi ini yang membedakan isolator, konduktor dan
semikonduktor.
Model pita energi ini
yang membedakan isolator, konduktor dan semikonduktor berdasarkan diagram pita
energi yang dimilikinya. Diagram pita energy tersebut adalah sebagai berikut:
Gambar Skema Pita Energi Isolator, Konduktor, dan Semikonduktor
Maknanya adalah sebagai
berikut:
1. Pita penuh, semua
electron statesnya terisi electron.
2. Pita yang secara sebagian terisi, ada
electron tereksitasi melampuai EF, tetapi masih berada dalam daerah
pita energy yang sama, electron yang tereksitasi tersebut meninggalkan
kekosongan dalam electron states dengan energy di bawah EF.
3. Pita yang hamper penuh, ada beberapa
electron states yang kosong karena electron hijrah ke pita energy di atasnya.
4. Pita energy yang hamper kosong, hanya
terisi oleh electron yang hijrah dari pita energy di bawahnya
5. Pita energy yang kosong sama sekali.
Skema untuk isolator:
1. Semua pita energy terisi penuh atau sama sekali kosong sehingga tidak
dapat terjadi konduksi.
2. Energi gap  cukup besar sehingga electron dari
pita energy yang penuh tidah dapat melompat ke pita energy yang kosong.
cukup besar sehingga electron dari
pita energy yang penuh tidah dapat melompat ke pita energy yang kosong.
3. Tingkat energy Fermi, EF melalui daerah harga energy yang
terlarang.
Skema untuk konduktor:
1. Tingkat energy Fermi EF melalui
pita energy yang diperkenankan sehingga pita konduksi setengahnya terisi dengan
electron.
2. Ada sebagian electron di atas EF
dengan meninggalkan electron states yang kosong di bawah EF,
konduksi terutama terjadi oleh electron.
Skema untuk
semikonduktor:
1. Tingkat energy Fermi EF,
melalui daerah harga energy yang terlarang sehingga pada suhu 0 K hanya ada
pita energy yang sama sekali penuh dan di atasnya pita energy yang kosong sama
sekali.
2. Celah energy  , tidak tinggi sehingga pada suhu T > 0 K yang cukup tinggi electron
dapat melompati beda energy
, tidak tinggi sehingga pada suhu T > 0 K yang cukup tinggi electron
dapat melompati beda energy  .
.
3. Karena electron yang melompat itu, ada
electron di pita konduksi yang kosong, sedangkan electron yang melompat itu
juga menciptakan kekosongan electron di dalam pita energy di bawahnya.
4. Pembawa muatan adalah electron dan
holes. Makin tinggi suhu makin banyak electron yang melampaui  maka konduktivitas zat makin
meningkat dengan kenaikan suhu. Ini adalah salah satu ciri utama dari zat
semikonduktor.
maka konduktivitas zat makin
meningkat dengan kenaikan suhu. Ini adalah salah satu ciri utama dari zat
semikonduktor.














Comments
Post a Comment